GNSS/Odometer/IMU integrated navigation system based on error state Kalman Filter
In this project, we want to estimate the kinematics of a moving vehicle/robot equiped with IMU, GPS and odometer. By integrating accelerometer and gyroscope reading from IMU unit, we are able to estimate the motion. However IMU integration leads to dead-reckoning position system which drift with time. In order to reduce accumulated error, on one hand we need to have a better understanding of the IMU reading influenced by bias and random walk of accerlerometer and gyroscope which change over time. Therefore besides kinematics, we need to estimate the bias and covariance of the measurement noise. On ther other hand, we need to fuse imu information with other source of info, such as the absolution position from GNSS reading and velocity from odometry.
One widely used method to fuse different source of sensor data is Kalman Filter. There are two key steps in classic Kalman Filter: prediction and correction. In the first step, IMU data effectively estimate the motion the system. To reduce the accumulated error from IMU integration, in the second step, the absolute position from GNSS and local velocity from odometer reading are fused with IMU reading to correct estimation. In this project a variation, i.e., error state Kalman filter is implemented. Instead of the system state, the variable of motion model and observation model in ESKF is the error state (i.e., the difference between true state and nominal state). Since the error state is small and close to the origin, it overcomes the limitations of classic KF such as sigularity, nonlinearity and large approximation error.
There are three parts of this project. First key functionality of the program is to covert the GNSS data (i.e. lattitude, longtitude, altitude, etc) to SE(3) pose whose origin is defined in UTM zone. Second, the basic routine to integrate IMU reading was implement to estimate kinematics. Last but not least, error state Kalman filter is implement for the state estimation.
GNSS data processing
-
Problem Statement:
- Given GPS data: time, latitude, longitude (deg), altitude, heading, heading_valid, orientation: north-east-down.
- Compute SE(3) pose whose origin is the first valid GNSS data.
-
Solution:
- Convert GNNS data to UTM data: zone, hemisphere, easting (x), northing (y).
- Change frame from antenna to body (IMU)
- Compute SE(3)
-
Components:
- Processor class: read, process and write data
- GNSS processor: conversion GNSS -> UTM -> SE(3)
- Visualization: Python script
- GNSS, UTM data class
- Main function: define GNSS process flow
- Processor class: read, process and write data
-
Program arguments:
- input data path
- output data path
- antenna pose: x, y, theta
IMU Integration
-
Problem Statement:
- Given IMU data: timestamp, gyroscope (angular velocity wx, wy, wz), accelerometer (ax, ay, az)
- Compute the state at each timestep position p, velocity v, rotation q, gyroscope bias b_g, accelerometer bias b_a, gravity g
-
Solution: simply integrate IMU data though the state will diverge pretty soon
-
Components:
- IMU data type, State type
- IMU integrator
- Processor class: read, process and write data
- IMU processor: simple integration
- Visualization: Python script
- Main function: define IMU process flow
-
Program arguments:
- input data path
- output data path
Error stata kalman filter
- Problem Statement:
- Given IMU, GNSS, Odom data, estimate the state at each timestep (p, v, q, ba, bg, g)
- Solution: implement error state Kalman filter
- Component:
- IMU data type, State type
- Odom data type: left wheel impulse, right wheel impulse, radius, impulse number per revolution.
- GNSS, UTM data class
- Processor class: read, process and write data
- Main function: define data processing flow
- IMU initializer: estimate initial mean accelerometer and gyroscope bias, and covariance
- ESKF: prediction with imu data, correction with odom and gnss data, reset error state and update covariance of the state
- GNSS data observe and correct position and orientation (only when heading angle is available)
- Odom data observe and correct the veloicty
- Visualization: Python script
- Program arguments:
- input data path
- output data path
- antenna pose: x, y, theta
- sensor fusion options
Estimation results
One of the benefit of sensor fusion with gnss, imu, odom data is the robustness which enables the system to work in different environment. For example imu sensor data helps to estimate the system state in GPS-denied environment. With the help of accelerometer and gyroscope data, the motion can be estimated in GPS-denied environment. Meanwhile GPS and odom data helps to reduced the accumulated error of IMU integration, e.g., the correction step of kalman filter. The figure below shows the GPS-denied region (scatter plot):
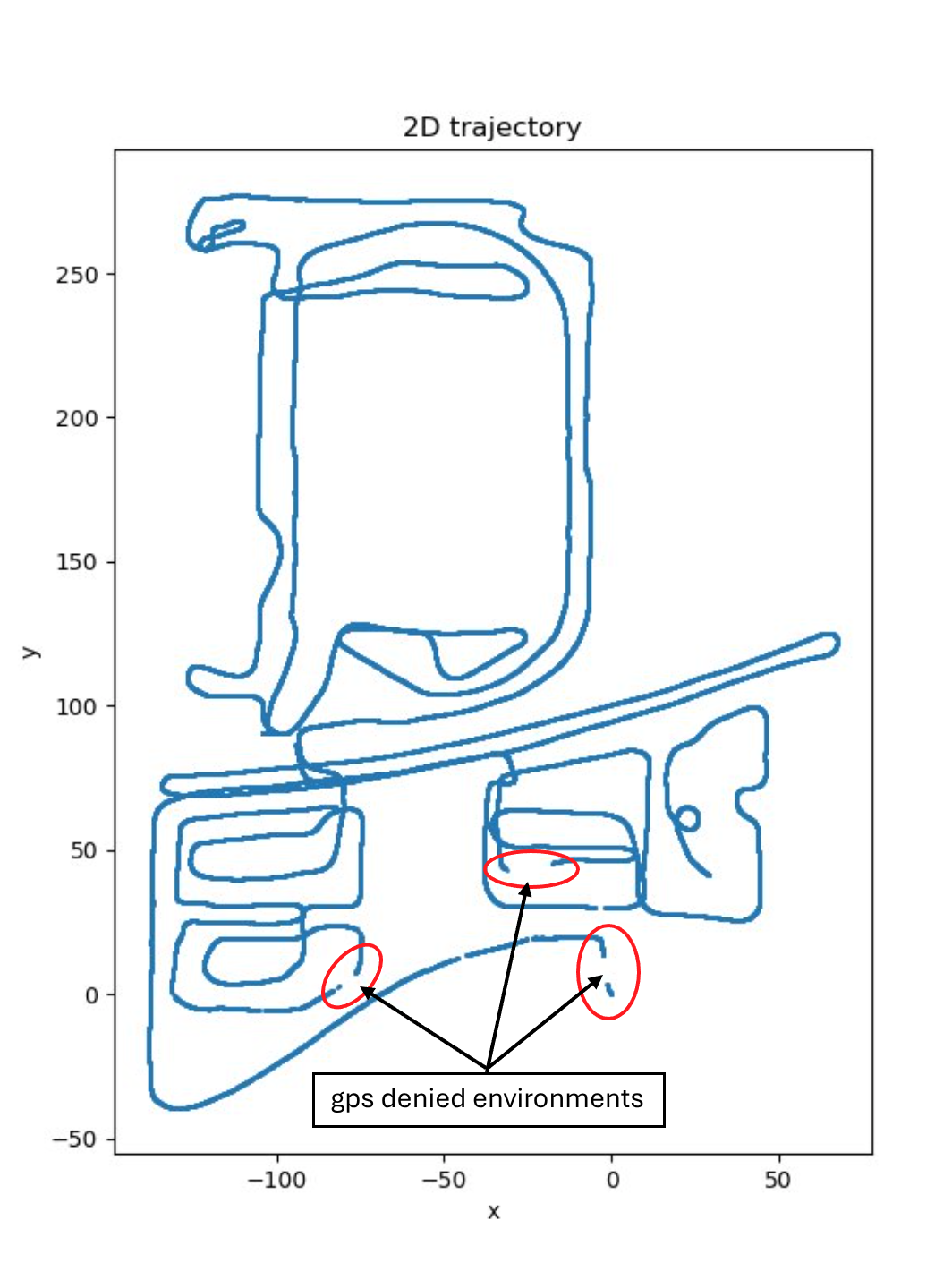
Due to the sensor fusion of IMU, GNSS and Odom data, the ESKF is able to estimate the motion in the GPS-denied region. The figure below shows that the gap is filled with imu and odom data by sensor fusion.
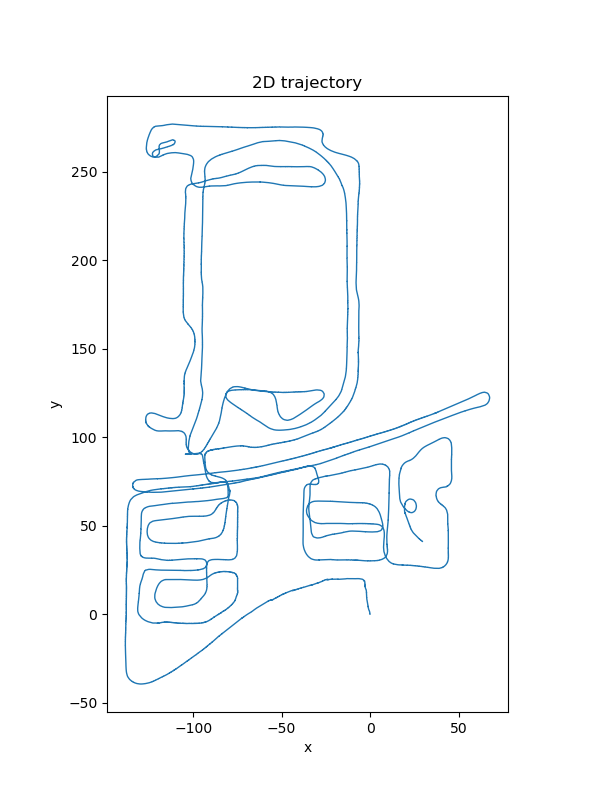
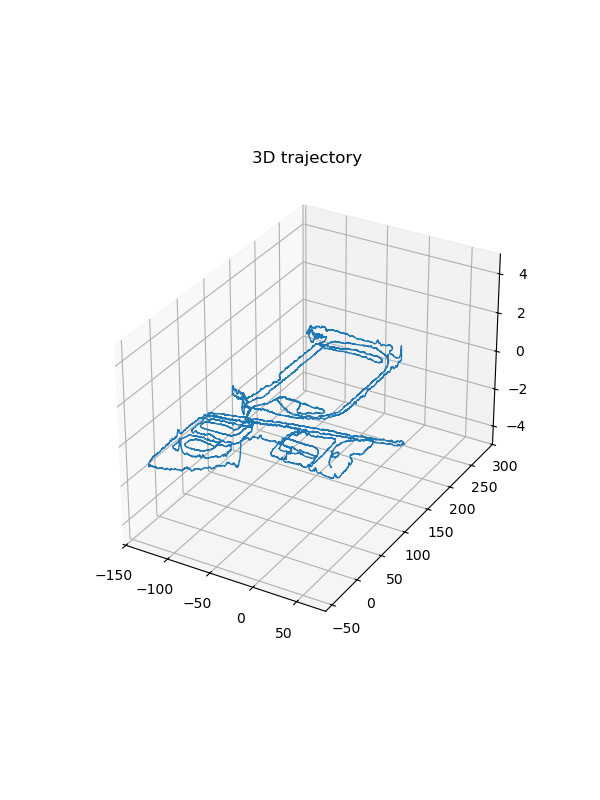
Let’s see what if we only integrate IMU data without fusing GNSS and Odom data.
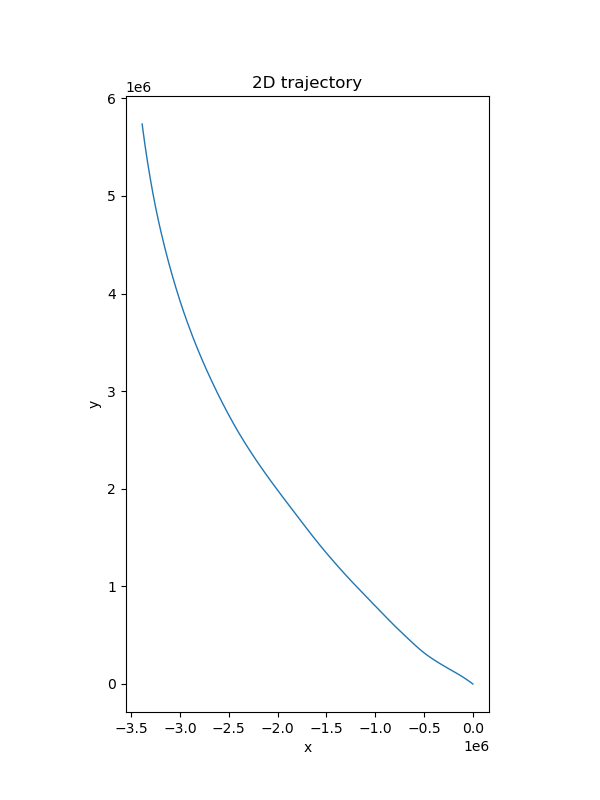
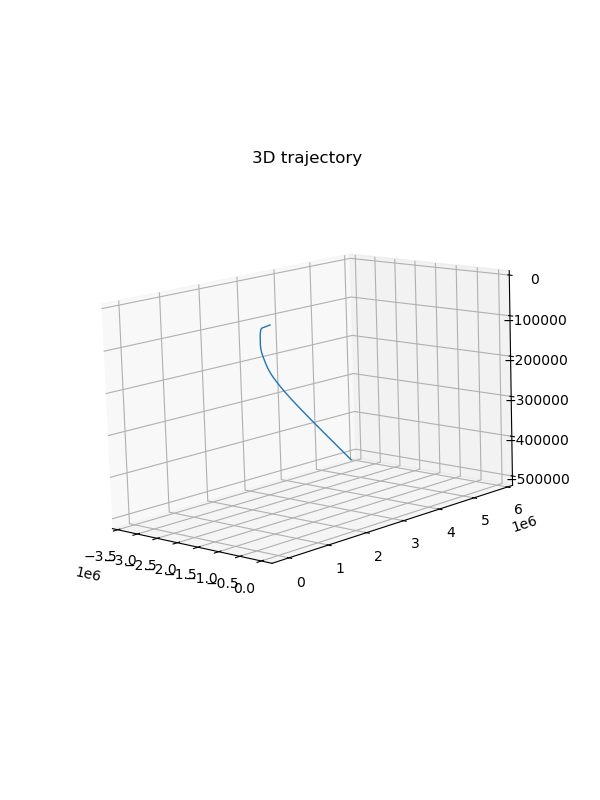
As we discussed at the beginning, the trajectory drift significantly.
Results of a different data set:
-
ESKF estimation
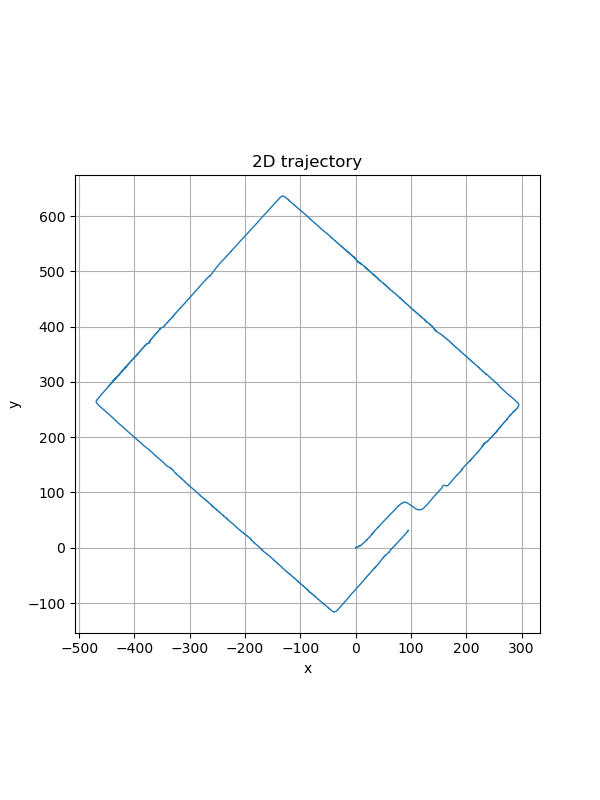
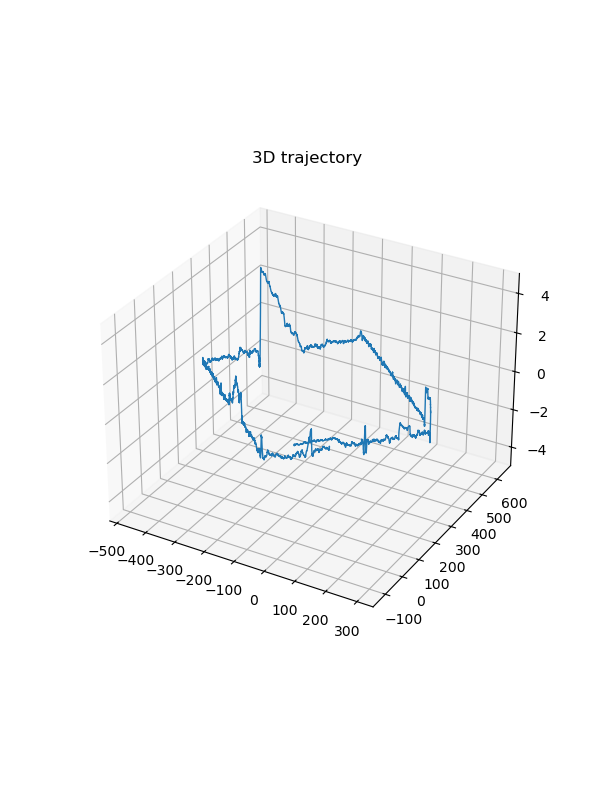 Trajectory estimation from ESKF
Trajectory estimation from ESKF -
Only IMU integration
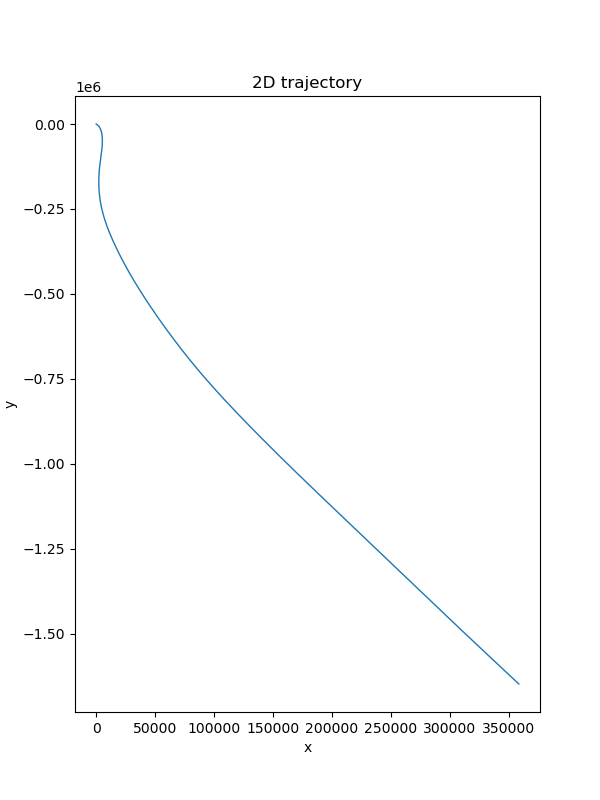
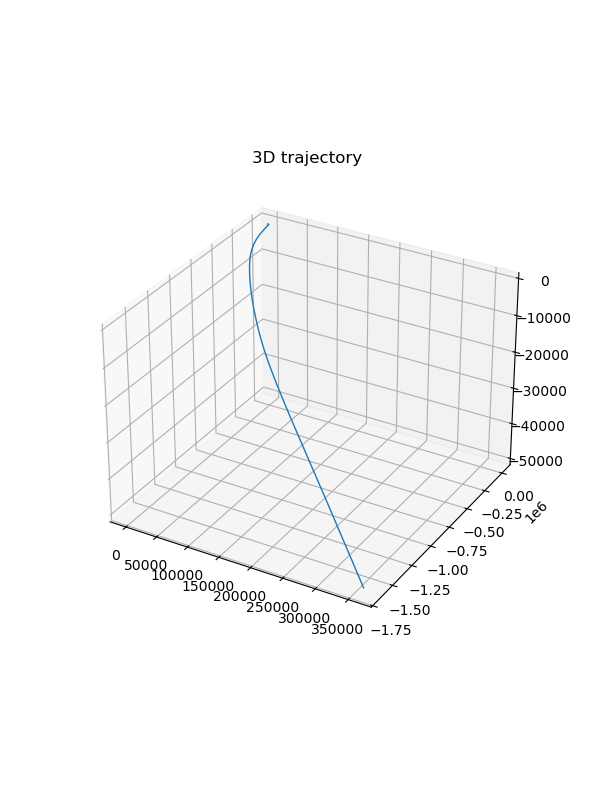 IMU integration only
IMU integration only