Particle Filter for Localization

Particle filter is a nonparametric filter which represents the posterior by a set of weighted samples. Since the functional form of the posterior is not needed, it can model arbitrary distribution, e.g., non-Gaussian distributions.

In this project, a complete particle filter is implemented using Python. Given the range-only sensor readings, odometry of robot and the ground-truth position of landmarks[1], robot uses a set of particles to represent the possible poses and an arrow to represent the average coordinates.

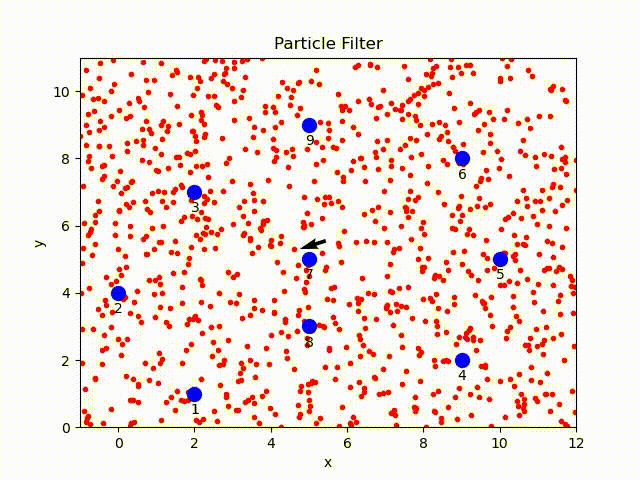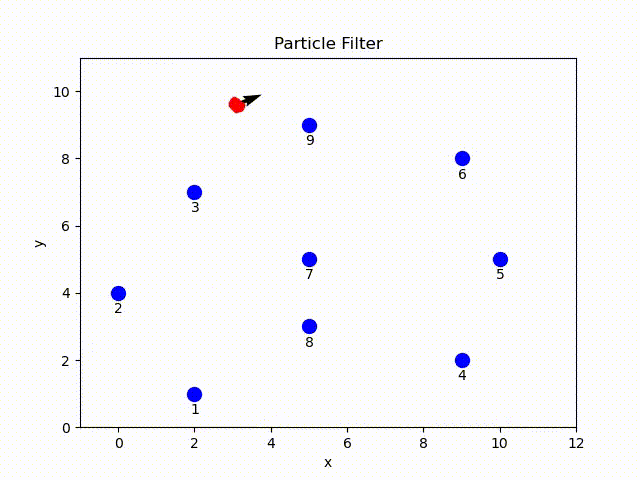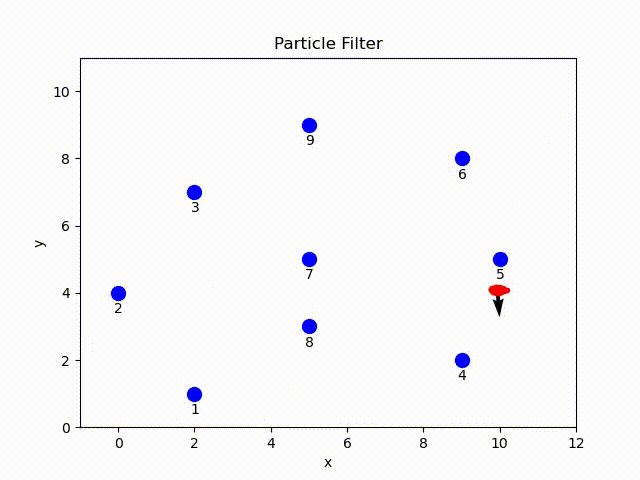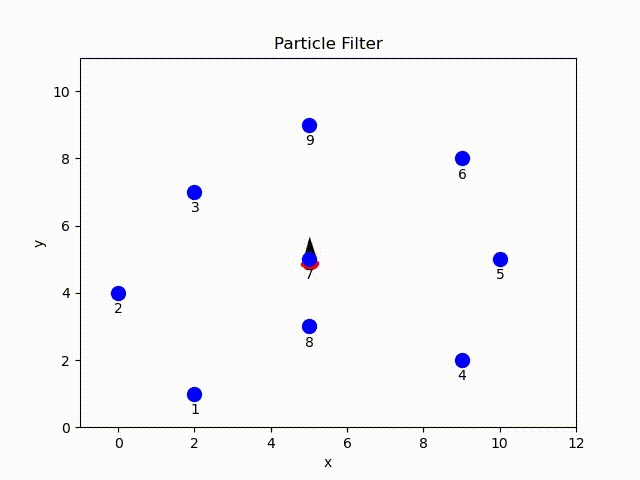
Particle Filter

Particle Filter Overview

Particle filter is an implementation of recursive Bayesian filter below:

\[\begin{equation*} \begin{split} bel(x_t) &= p(x_t|z_{1:t}, u_{1:t}) \\ & = \eta P(z_t|x_t) \int_{x_{t-1}} P(x_t|x_{t-1}, u_t) bel(x_{t-1}) \mathrm{d}x_{t-1} \end{split} \end{equation*}\]

The posterior \(p(x_t|z_{1:t}, u_{1:t})\) is represented by a set of weighted samples, i.e., \(\chi = \{\langle x^{[j]}, w^{[j]} \rangle\}_{j=1,...,M}\)

  1. In each time step, the particles are propagated based on the motion model \(P(x_t|x_{t-1}, u_t)\).
  2. Then they are weighted according to the likelihood of the observation \(P(z_t|x_t)\).
  3. In the resampling step (importance sampling essentially), new particles are draw with a probability proportional to the weights, which account for the difference between the proposal and target distribution.

The pseudocode[2] is presented below:

Particle Filter


Code Explanation

There are three key functions in this implementation.

  1. sample_motion_model(odometry, particles): take as inputs the odometry and the current set of particles, sample new particles based on the odometry motion model and the motion noise. The pseudocode[2] is presented below.
    Sample New Particles

  2. eval_sensor_model(sensor_data, particles, landmarks): given the sensor readings, partcles sampled from motion model, the ground-truth position of landmarks, measurement noise, compute the weights of samples from observation models, i.e., \(w_t = P(z_t|x_t)\).

  3. resample_particles(particles, weights): draw with replacement \(M\) (size of particle set) particles from the given set with probability equal to the weight. The resampling is implemented by the low variance resampling with linear complexity.
    Low Variance Resampling


References

  1. Introduction to Mobile Robotics
    University of Freiburg, Spring, 2020, http://ais.informatik.uni-freiburg.de/teaching/ss20/robotics/index_en.php.

  2. Probabilistic Robotics
    S. Thrun, W. Burgard, and D. Fox. MIT Press, Cambridge, Mass., (2005)