Mobile Robot Collision Avoidance using Reinforcement Learning

In this project, I use Deep Deterministic Policy Gradient (DDPG) to train multiple mobile robots to avoid the obstacle. Given the range sensor readings (states) that detect obstacles in the map, robots learn a policy to control linear and angular velocity (actions) to avoid the colliding into obstacle.

Overview of DDPG

DDPG is a model-free, off-policy, online, actor-critic learning algorithm. It uses the deep neural network to learn deterministic policies in high-dimensional, continuous action space. It combines the idea of Deep Q-network and Deterministic Policy Gradient. Like DQN, it uses replay buffer to address the correlation in the sequence of observations. It uses the deterministic policy gradient theorem from DPG to compute (approximate) the gradient of cumulative long-term reward with respect to the actor parameter.

DDPG contains four function approximators:
(1) Actor network \(\mu(s|\theta^{\mu})\): take observation \(s\) and return action that maximize cumulative rewards.
(2) Target actor network \(\mu'(s|\theta^{\mu'})\): improve the stability of the learning; the parameter \(\theta^{\mu'}\) is updated slowly.
(3) Critic network \(Q(s,a|\theta^{Q})\): take observation \(s\) and action \(a\), return action-value.
(4) Target critic network \(Q'(s,a|\theta^{Q'})\): improve the stability of the learning; the parameter \(\theta^{Q'}\) is updated slowly.

Both target actor \(\mu'\) and \(Q'\) change slowly, the learning therefore is close to a supervised learning. Specifically, \(\mu'\) and \(Q'\) are used to compute the target value and \(\mu\) and \(Q\) compute the value the current network returns. The difference of value and target value are used to adjust the parameter in \(\mu\) and \(Q\).

The pseudocode is following:

1. Initialize critic network \(Q(s,a|\theta^{Q})\) and actor \(\mu(s|\theta^{\mu})\).

2. Initialize target critic network \(Q'(s,a|\theta^{Q'})\) and actor \(\mu'(s|\theta^{\mu'})\), the parameter is same with the critic and actor network.

3. For each episode

   • For each time step
     1. Select action based on the current actor and exploration noise, i.e., \(a_t = \mu(s_t|\theta^{\mu}) + \mathcal{N}_t\).
     2. Execute action, observe reward \(r_t\) and new state \(s_{t+1}\).
     3. Store transition \((s_t, a_t, r_t, s_{t+1})\) in replay buffer.
     4. Sample a random minibatch of \(N\) transition \((s_i, a_t, r_i, s_{i+1})\) from buffer.
     5. Compute target value \(y_i = r_i + \gamma Q'(s_{i+1}, \mu'(s_{i+1}|\theta^{\mu'})|\theta^{Q'})\).
     6. Update critic by minimizing the loss \(\frac{1}{N} \sum_i (y_i - Q(s_i,a_i|\theta^Q))^2\).
     7. Update actor using sampled policy gradient \(\nabla_{\theta^{\mu}}J \approx \frac{1}{N} \sum_i \nabla_a Q(s,a|\theta^{Q})|_{s=s_i, a=\mu(s_i)} \nabla_{\theta^{\mu}} \mu(s|\theta^{\mu})|_{s=s_i}\).
     8. Update the target networks
        \(\theta^{Q'} \gets \tau\theta^Q + (1-\tau)\theta^{Q'}\); \(\theta^{\mu'} \gets \tau\theta^{\mu} + (1-\tau)\theta^{\mu'}\)

Simulation Model

The Simulink model is shown in figure below. This is a standard reinforcement learning setup consisting of agents interacting with envrionment in discrete timestep. At each time step t, the agents take action based on the observation. As a consequence of the action, the agents receive reward and find themself in new states.

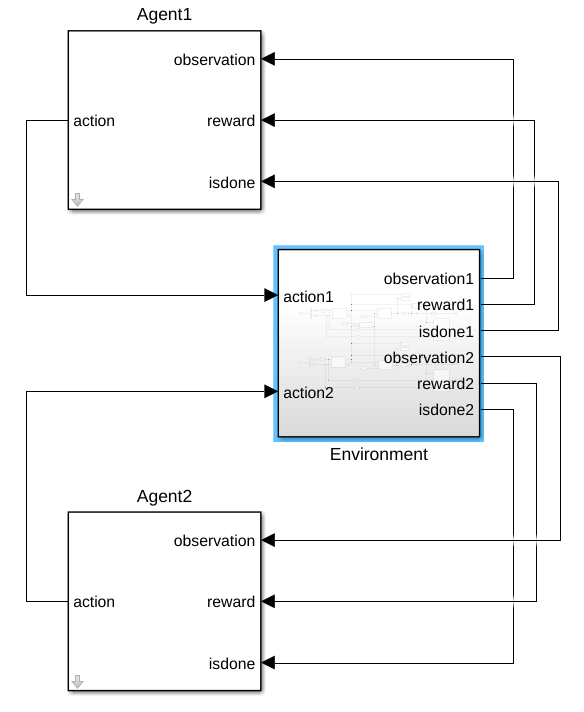
In more details, in each agent we define the training networks using the specified deep neural network , i.e., actor and critic shown in figures below.

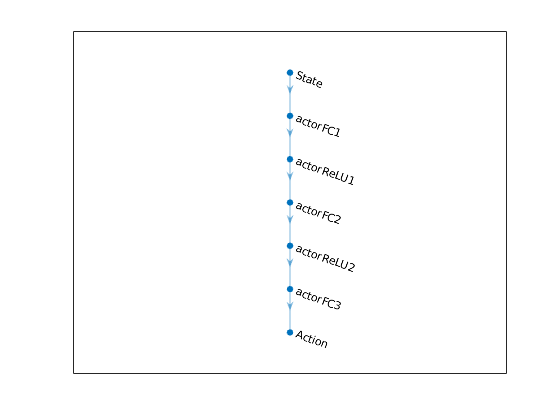
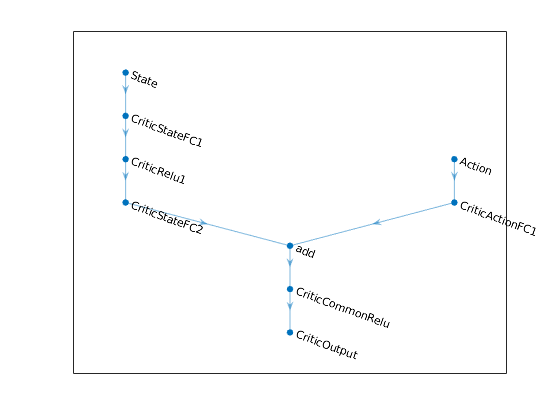
The state is defined as a vector of 7 continuous variables ranging from 0 to 12. The action is defined as a vector of 2 continous variables ranging from -0.3 to 0.3.

In the simulation envrionment below, we define the reward function and the transition function.

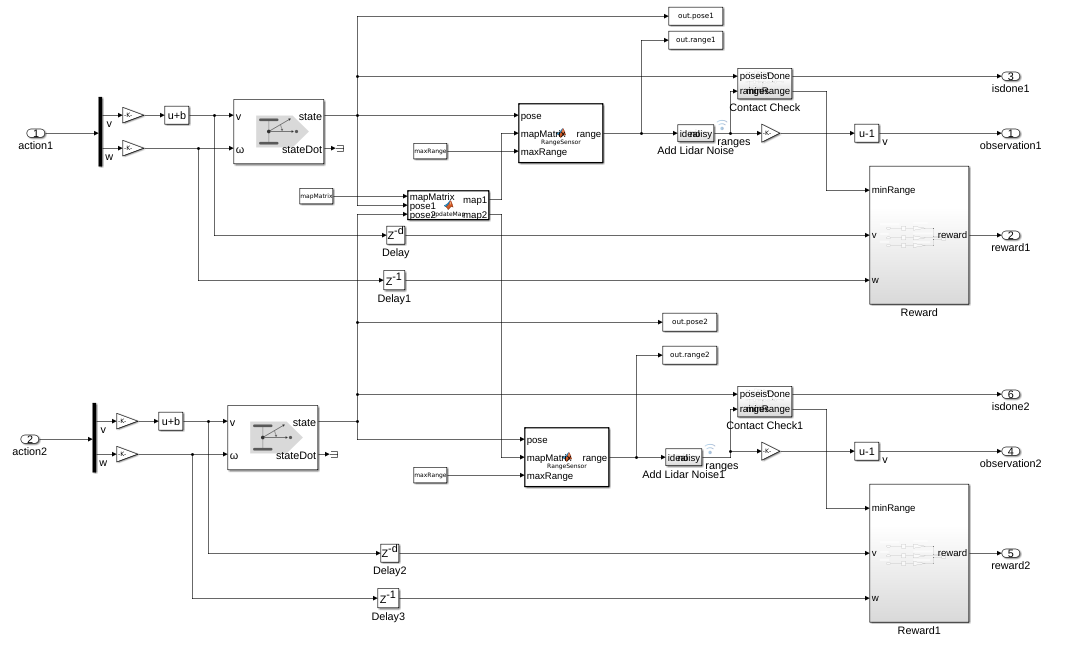
Given the action returned by the policy, the differential-drive mobile robot model differentialDriveKinematics produces the current pose, which is sent to the rangeSensor function. Then the sensor readings are sent to robot. This part of model works as the transition function in MDP.

In order to make robot avoid the obstacle, a reward function is defined as

where \(d\) refers to the minimum distance to the obstacle obtained from the sensor reading, \(v\) and \(w\) denote the linear and angular velocity. \(\alpha\) and \(\beta\) are positive coefficient. \(\lambda\) is negative to avoid robot rotating at same location.

In addition to the transition function and reward function, a contact-check module is used to detect if any of robots colliding with obstacle. If the collision happens, the current episode terminates.

Training results

The object of the training in this project is to enable mobile robots to avoid the obstacle. So the robots are supposed to move randomly without collision until the sample time end (which is defined to be 1000 time step). As shown in figures below, the performance of mobile robot is getting better, and the episode reward and elapsed time increase.

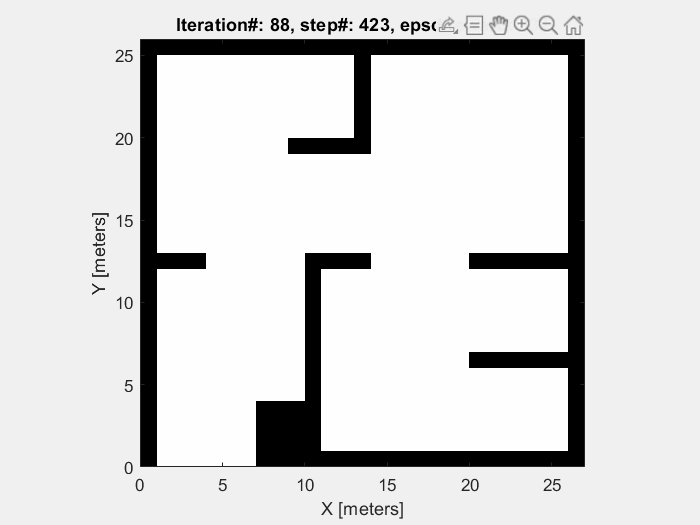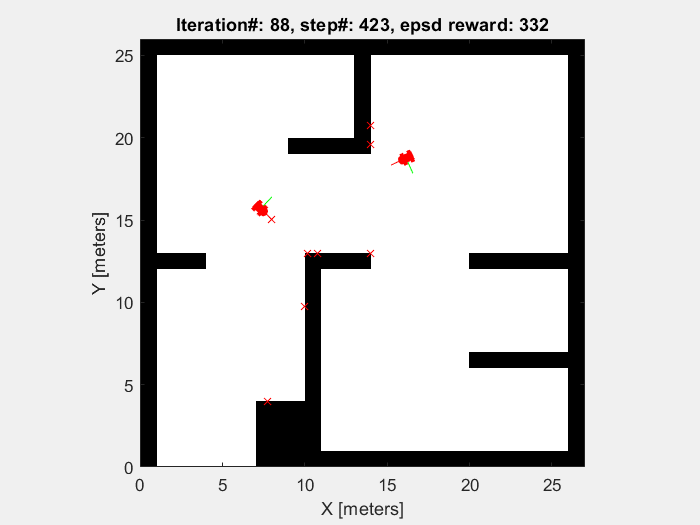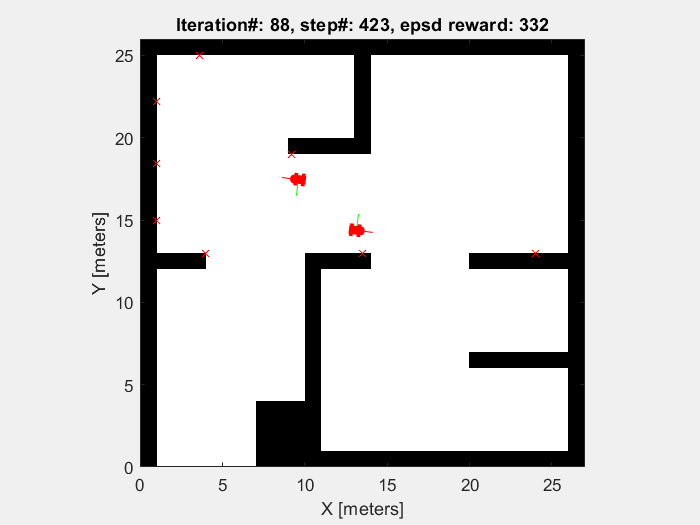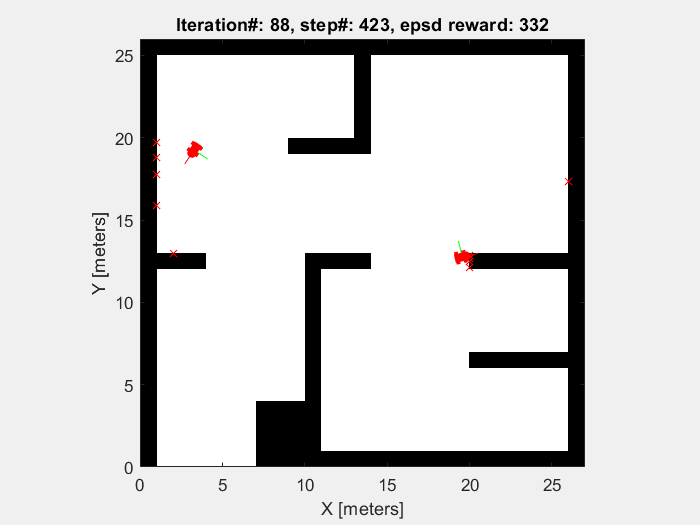
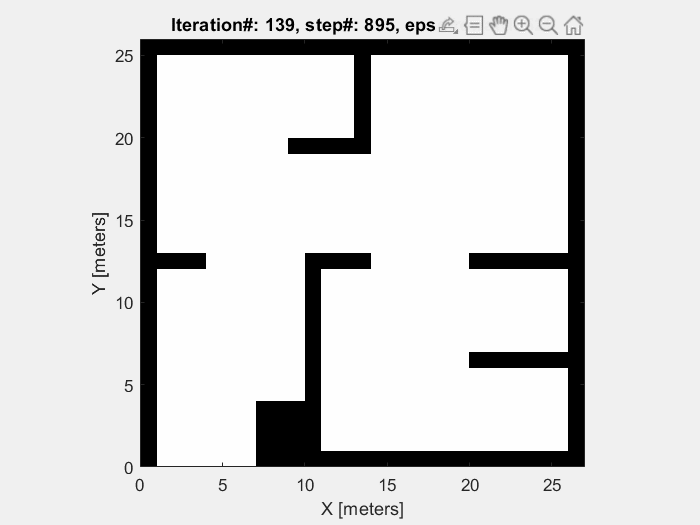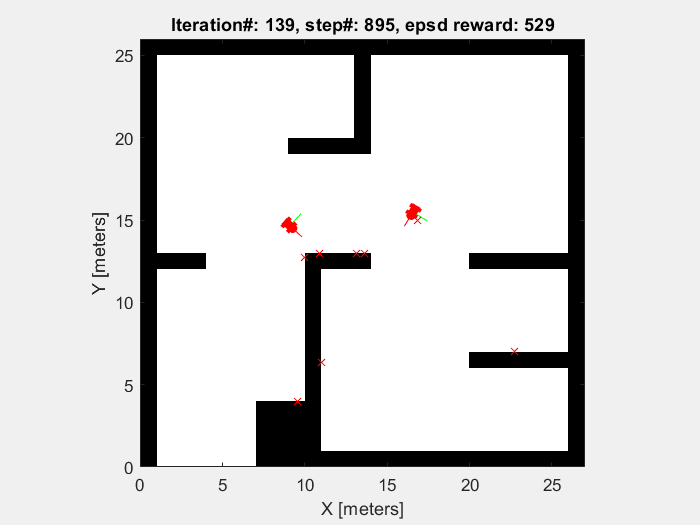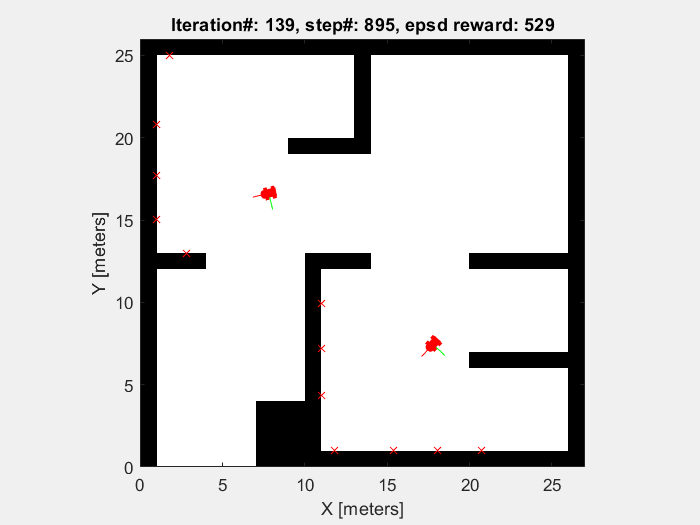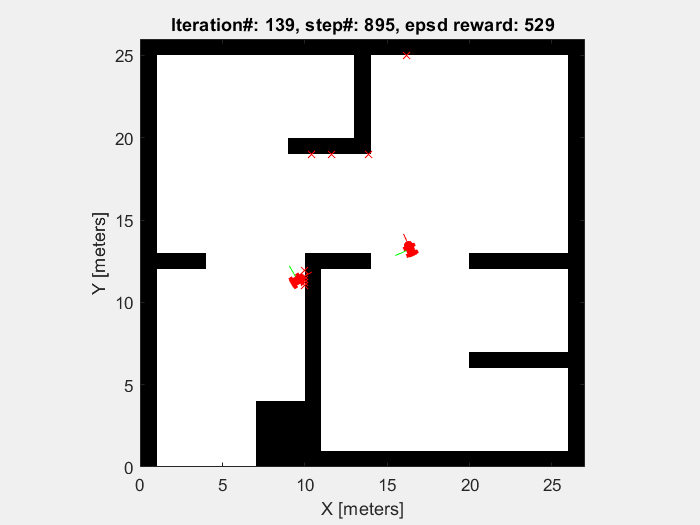
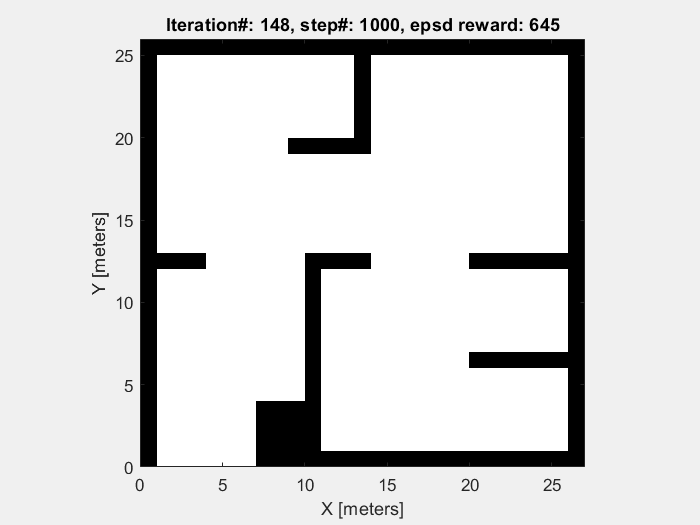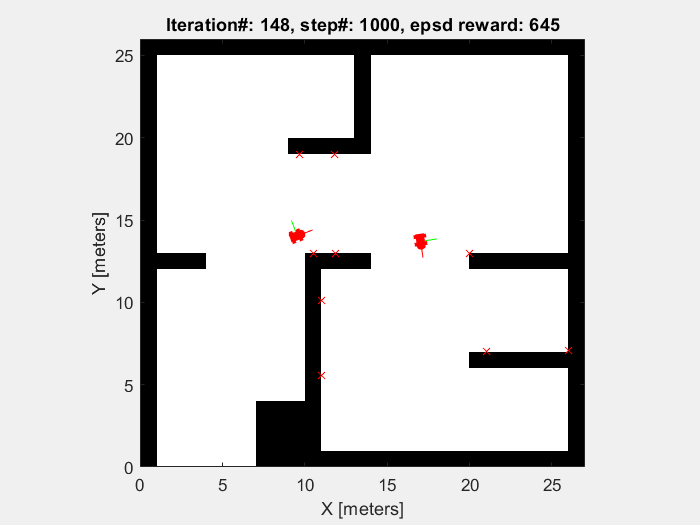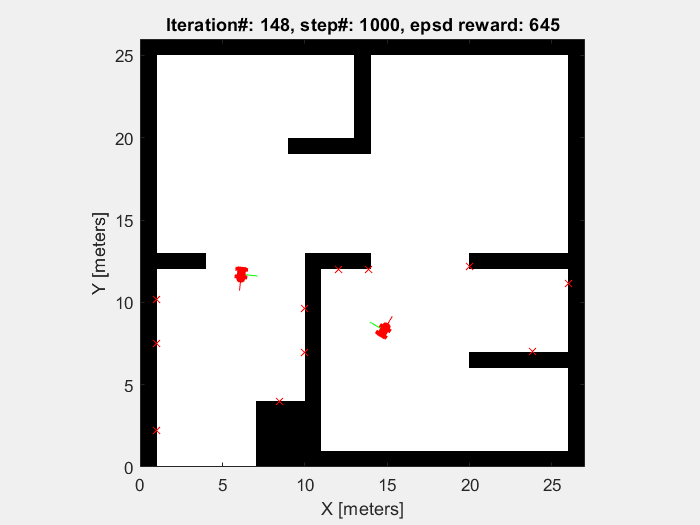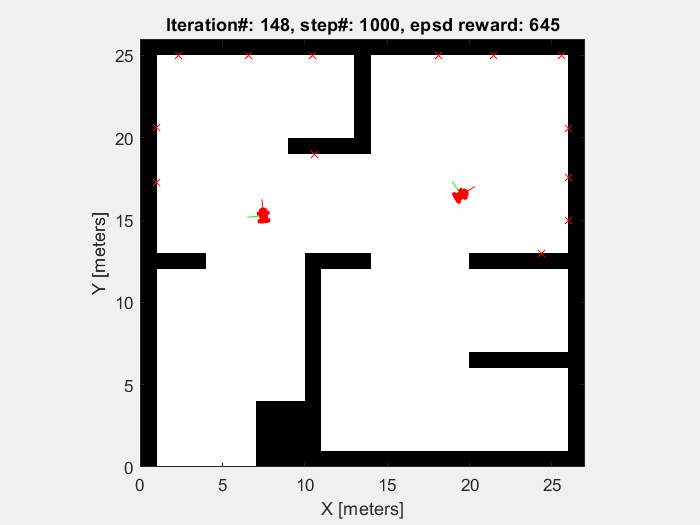
Running

To run the simulation, first create the variables used in the agent and environment, e.g., robot parameters, range sensor parameters. Type following command in command window. createEnvMulti

Then set up training parameters like sample time, discount factor, minibatch size, and perform training.
trainAgentMulti

After the training, perform the simulation with the trianed robots and visualize the results.

out= sim('MultiMobileRobotObstacleAvoidance.slx');
showResults;

A trained agent is included in the repository. To see the result without training:
trainedAgentDemo