research
Multi-robot system has a wide range of applications including collaborative autonoumous manufacturing, automated warehouses, search and rescue. Despite the advantages like robustness and reliability, multi-robot system is usually complex and often influenced by the uncertain environment. My research focuses on developing algorithms for multi-robot system that will coordinate robots to work robustly and reliably under highly uncertain environment.
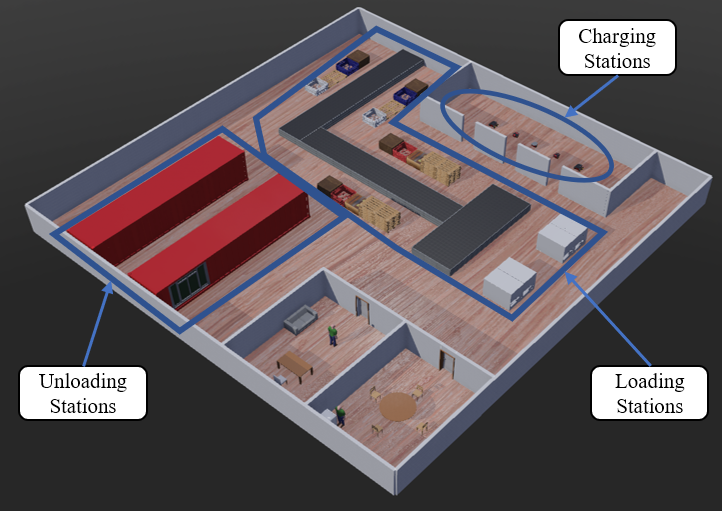
The problems studied in my research can be illustrated by following motivating examples. The first example is the point-to-point object transfer. Imagine in an automated warehouse, a team of robots are initially located at charging stations. The packages are located at loading station. Each robot has to pick up packages from the loading station and deliver it to the unloading station for storing and processing. There is a resource budget for each robot delivering packages. Robot obtains certain amount of payoff for accomplishment of package delivery. We need to assign packages to each robot and compute path for each robot from its charging station to loading station and unloading station such that the team performance (total payoff) is optimized.
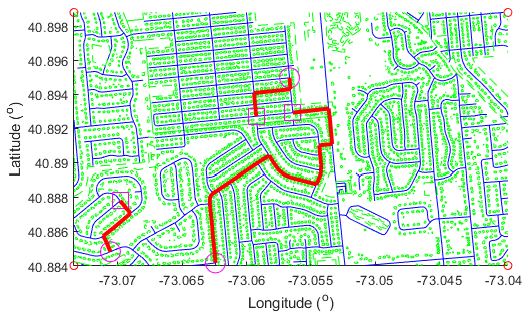
The second motivating example is the mobility-on-demand. As shown in figure below, a number of passengers are initially located at places marked by squares and a team of autonomous robots are initially located at places marked by circles. Passengers are calling for pick-up. Each robot should be assigned to a passenger and compute a path to pick up the assigned passenger. The goal is to have a minimum amount of time taken by the robot team to pick up all passengers successfully.
Two problems are involved in these two examples: multi-robot task allocation and multi-robot path planning. The formal definition of multi-robot task allocation is: Given a set of robots and a set of tasks with each robot obtaining some payoff and consume resource for each task, compute a subset of tasks for each robot such that a team performance criteria is optimized subject to a set of constraints on the tasks and/or the robots. Current literature on multi-robot task allocation usually consider the problem parameters like payoff and resource consumption as the deterministic value. However in practice robots have to deal with enormous uncertainty that exists in the phsical world. There are many factors that contribute to the uncertainty, such as robot environment, sensor and actuation. For example, the energy consumption for robot picking up passengers may not be known exactly due to the uncertain traffic condition. The robot may go off the planned path to avoid uncontrolled obstacles in the warehouse. Therefore the goal of my reasearch is to formulate multi-robot task allocation problems with parameter uncertainty and develop solution algorithms that provide probabilistic guarantee.
The formal definition of multi-robot path planning is: Given the initial and goal position of a team of robots, compute a collision-free path for each robot from its initial position to its goal poisition. Current literature of path planning focus on the closed environment where all static and moving obstacles are under control of the system. The degree of uncertainty in such well-structured environment is small. However in many scenarios such as high way and private homes, environment is highly dynamic and in many ways highly unpredictable. The uncertainty is particularly substantial for robots operating in the proximity of people. A part of my research studies the multi-robot path planning under highly uncertain open environment.
More importantly, in practice the robots have to both allocate the tasks among themselves and plan a collison-free path to the assigned tasks, as shown in those two examples. Although it is convenient to find a solution by decoupling, there is no guarantee that the solution is optimal especially when environment is highly uncertain. In my research, I focus on simultaneously computing the allocation of tasks to robots as well as planning their paths as a single problem. This is done while considering the stochasticity of the path costs and assuming the uncertain open environment.
The key contribution of my research is to develop a unified methodology of solving multi-robot task allocation and path planning with uncertainty in payoffs (costs) and resource consumption.
Linear Assignment problem with the uncertain payoffs
The linear assignment problem is the basic version of the multi-robot task allocation in which each robot performs exactly one task. It is assumed that the paths from robots to tasks are given to us (e.g. prm is used to compute paths in figure above). The path cost (more generally assignment cost or payoff) is random variable with known mean and variance. The goal is to find the solution that optimizes the stochastic total team cost (payoff).
The problem is formulated as a chance-constrained problem which provide us the flexibility to tradeoff between performance and reliability. I devise centralized and distributed algorithms that compute the optimal assignment with a priori probabilistic guarantee on team performance. The primary contribution is the development of the connection between the chance-constrained problem and risk-averse problem.
Chance-constrained Simultaneous Task Allocation and Path Planning
This problem can be illustrated by the mobility-on-demand example. A team of robots and passengers are initially located at known places. The robots are moving in an open environment where there are other uncontrolled mobile agents that occupy the space. The environment is represented by a graph which captures the collision-free configuration space of the robots. The travel cost of robot are stochastic. The goal is to assign robots to passengers and compute a path for each robot to the assigned passenger’s location such that the total travel cost of robot team (which is stochastic) is optimized.
In our ICRA 2020 paper, we present distributed algorithms that solve the problem optimally. We prove that the optimal solution can be obtained from a deterministic version of the problem. In particular, the travel cost in deterministic problem is a linear combination of the mean and variance of the random cost in the stochastic problem. The challenge is to find the proper coefficient of the linear combination (i.e., risk-averse parameter) so that the equivalence holds.
Chance-constrained Simultaneous Task Allocation and Path Planning with Bottleneck Objective
In many applications, instead of the sum of the individual robot’s performance, we care about the bottleneck performance of the robot team. For example, the robot team should complete the tasks in a minimum time window. The problem has similar assumptions to the problem above. The difference is that objective of the optimization is MinMax, i.e., minimize the maximum picking up time of the robot in the team.
In ICRA 2021 paper, we propose a method that decompose the problem into two sub-problems, i.e., chance-constrained shortest path problem and linear bottleneck assignment problem. We prove that the optimal solution can be computed by solving a linear bottleneck assignment problem in which the assignment cost is equal to the objective of the chance-constrained shortest path problem. Leveraging the idea from the chance-constrained linear assignment problem, we design algorithms to solve chance-constrained shortest path problem optimally. The actual cost of the obtained path is guaranteed to be lower than a minimized threshold value with high probability.
Chance-constrained Knapsack Problem with Applications to Multi-Robot Perimeter Patrolling
We study a perimeter patrolling application by a team of quadrotors in which the robots with limited battery life have to move along a route of a given length. It is assumed that the length to be covered is much larger than the distance an individual robot can fly. Due to the uncertain environment, the distance an individual robot can travel is stochastic. There is an operating cost for each robot. We are given a group of heterogeneous robots. The goal is to select a team of robots of minimum total operating cost to cover the route with high probability.
The problem is formulated as a chance-constrained knapsack problem in which the knapsack size refers to the route length and the weight of item is the stochastic travel distance of robot. We design an iterative algorithm to solve the chance-constrained knapsack problem optimally by methodically solving a sequence of risk-averse knapsack problem. We prove that the optimal solution of chance-constrained problem is also optimal to the risk-averse problem with proper value of risk-averse parameter and route length. The problem thus boils down to a two-dimensional search on risk-averse parameter and route length.
Generalized Assignment Problem with Stochastic Resource Consumption
We study a task allocation problem with random resource consumption. A team of robots should pick up parts from a clustered storage location and deliver it to processing stations. The resource consumption refers to the energy consumed by each robot to travel between the storage location and processing station, which is stochastic. There is a resource budget for each robot. Robots can perform multiple tasks as long as resource budget is not violated (e.g., delivering parts multiple times). The goal is to assign tasks to robots such that the total payoffs of the robot team is maximized and the resource budget for each robot is not violated with probabilistic guarantee.
The problem is formulated as a generalized assignment problem with chance constraint on the resource consumption. It is a geralized form of the chance-constrained knapsack problem, in that each robot can be treated as a knapsack. In IROS 2020 paper, we present an (1+α) approximation algorithm in which each robot solves a chance-constrained knapsack problem sequentially. We also devise an α-approximation algorithm for chance-constrained knapsack problem which uses any α-approximation algorithm for deterministic knapsack problem as a subroutine. The solution of the generalized assignment problem is proved to be (1+α) approximaton (which is 2 if the chance-constrained knapsack problem is solved optimaly).